Triad chords that sound good when played together.

Using substitution chords. [Beginner lesson]

One of the best ways I know how to learn basic triad chords and their progressions, is to experiment with using substitutions chords. How do you know which chords sound good when they are played together? How can you figure out which chords to choose? Well, you kind of have to know a little bit about basic music theory to figure this out. This article takes a look at what you need to know, and how to use the process of availability in order to figure out songs and write your own songs.

---

What are some of your favorite, easiest chords?

Just about everyone who ever picks up a guitar, has learned a few of the basic "cowboy" or open-string chords. These include in no particular order:

"C, G, D, Em, Am, F, Dm, A, E, C7, G7, D7, E7, Em7, A7, B7 and Am7"

If you know how to play even half these chords, you can already play hundreds of songs. 

Most people who know some or all of these chords, might have no idea why they are called what they are called, or where they even come from. They don't just magically exist out of thin air on your guitar, right? There must be some sort of musical organization for these chords to make sense in a group or a family, right?  Yes there is.

They're called "Keys". 

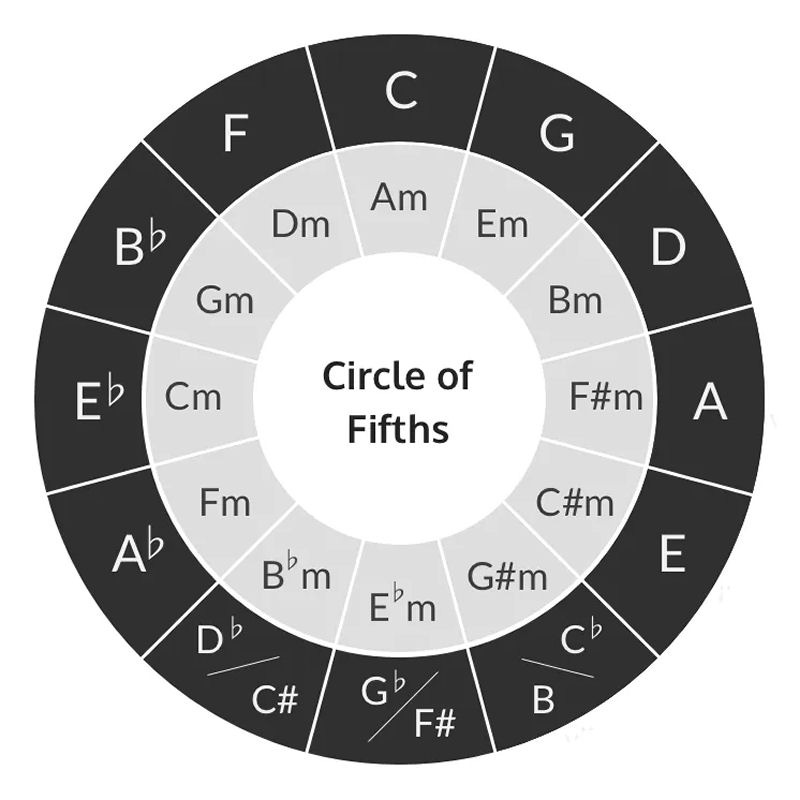
You need to know your keys. (Not keys on the piano). You need to know some basic music theory. Let's take a look at the diagram below. This is called the "Circle of 5ths". This is where all of the keys and all of your basic chords originate.

Let's outline this in a linear perspective. Since most of the easiest cowboy chords exist in the key of C major, let's use that key.

Key of C major

"C, Dm, Em, F, G and Am". (We'll skip using the B diminished chord for this exercise).

If you play any of these six chords in any progression, they will sound good together. There are combinations of chord progressions that sound better than others. 

For example: "C - Am - F - G" or "C - Am - Dm - G". Why do these chords work so well together? Every key has a specific series of seven notes called a "major scale". 

Perhaps you've watched the classic Julie Andrews movie called "The Sound of Music". In this movie, she regales us with a song about learning notes in a scale by using the "Do-Re-Mi-Fa-So-La-Ti", then back to the "Do" method.

This is arguably the most common scale in music. When you apply musical notes to each of the two-letter words in the scale, you find that every scale uses (some form of) the first seven letters from the alphabet: A, B, C, D, E, F and G.

If we use the key of C major to do this, the notes will look like this:

"C = D, D = Re, E = Mi, F = Fa, G = So, A = La and B = Ti".

We can use these notes to construct chords in a key. In order to do this, we need to use a building formula to make the chords in the key. We'll start off with the first chord in the key of C major.

C (Major)

C requires the 1st (Do), 3rd (Mi) and 5th (Fa) notes in the key of C. These notes are "C, E and G". We can literally place the structure of these notes in any order to build the C chord. It does help however, to keep the root note "C" as the lowest note, but it isn't completely necessary.

D (minor)

D minor requires the next three notes: "D, F and A"

E (minor)

E minor requires the next three notes: "E, G and B"

You can begin to see the pattern forming here, right? The rest of the chords in the key will be built using the same pattern.

Families of chords

When you understand where chords actually come from, how they belong to groups or families of chords, you can begin to understand why they sound good when played together in a progression. This is because all of the chords from a key come from the same notes in the key. However, we are not limited to using the chords in just one key. You can use many other chords from other keys to create songs.

If you look at the circle of 5ths diagram above, you can see that to the left and right of the key of C major, are the keys F major (left) and G major (right). Both of these keys share common notes and chords with the key of C major. This means that if needed, we can use some of the chords in those keys to add to our key of C major when building a chord progression.

For example, if we use the common chords in the keys of C and F major, we find that these chords are: "F, Am, C and Dm". We also have access to the other two chords in the key of F major: "Gm and Bb".

Going the other way, if we use the common chords in the keys of C and G major, we find that these chords are: "G, Am, C and Em". We also have access to the other two chords in the key of G major: "Bm and D".

So, relatively speaking, we have a lot more chords to play with, than just the handful we have in our key of C major. We actually have ten chords available (not including the diminished chords).

Substitution chords

You can even use replacement (substitution) chords to change things even more. For example, if you play the progression "Am - F - C - G" and replace the "G" with an "Em" it might sound okay. But, how about if you switched that Em to an "E major"? This is a trick used in a lot of songwriting. Instead of using the 5th chord from a key, you replace it with a major version of the 3rd chord from the key.

Here are some examples using the "vi - IV - I - V" and "vi - IV - I - III" chord progressions:

Key of F = "Dm - Bb - F - C " and "Dm - B - F - A"

Key of C = "Am - F - C - G" and "Am - F - C - E"

Key of G = "Em - C - G - D" and "Em - C - G - B"

Key of D = "Bm - G - D - A" and "Bm - G - F - F#"

Key of A = "F#m - D - A - E" and "F#m - D - A - C#"

Key of E = "C#m - A - E - B" and "C#m - A - E -G#"

Using the Major 3rd as a substitution chord to replace the 5th chord in the key, creates a sort of "tension" in the progression.

The more that you practice and understand your keys in music, and know what you have available, it will help you understand how songs are created, structured and written. This can be a powerful tool in learning how to figure out how to play your favorite songs and how to create and write your own songs.

Thank-you for taking the time to read this guitar lesson. If you enjoy my series on guitar lessons and would like to pledge your support, please consider an investment in a  monthly or yearly subscription. Thank-you!